Praktik məsələlərin həllində bəzən kəmiyyətlərin təqribi qiymətlərindən istifadə olunur. Ədədləri yuvarlaqlaşdırarkən, cihazla kəmiyyətləri ölçərkən təqribi qiymət anlayışı ilə tanış olmusunuz. İndi kəmiyyətin təqribi və dəqiq qiymətləri arasında olan xətanı araşdıraq.
- Dəmir və taxta xətkeş götürün. “Riyaziyyat 7” kitabının uzunluğunu hər iki xətkeş vasitəsilə ölçün. Alınan ədədləri yazın. Nəticələri müqayisə edin. Hər iki ölçmədə eyni nəticə alındımı?
- Dəqiq uzunluğun 24 sm olduğunu qəbul edərək dəqiq və təqribi qiymətlərin fərqinin modulunu tapın. Sizcə, aldığınız ədədi necə adlandırmaq olar?
-
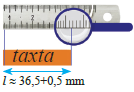
Taxta parçasının uzunluğu (l ) şəklə görə 3,6 sm və 3,7 sm arasında yerləşir. Deməli, l ≈ 36,5 + 0,5 mm = 37 mm və ya l ≈ 36,5 – 0,5 mm = 36 mm kimi yazmaq olar, yəni taxtanın uzunluğu 0,5 mm-ə qədər dəqiqliklə verilmişdir.
-
Burada ölçmə zamanı yol verilən xəta |37 – 36,5| = 0,5 mm və ya |36 – 36,5| = 0,5 mm hesab edilir.
Kəmiyyətin dəqiq (a) qiyməti ilə təqribi (x) qiymətinin fərqinin modulu təqribi qiymətin mütləq xətası adlanır. Δ = |a - x|
Mütləq xəta = |dəqiq qiymət – təqribi qiymət|
Mütləq xəta ölçmələr nəticəsində alınan təqribi qiymətin kəmiyyətin həqiqi qiymətindən nə qədər fərqləndiyini göstərir.
a ≈ b olarsa, kəmiyyətin dəqiq qiyməti üçün |a – b| < a < a + b ikiqat bərabərsizliyi ödənir (burada a > 0).
5,019 ədədini yüzdə bir və onda bir dəqiqliyi ilə yuvarlaqlaşdırın. Yuvarlaqlaşma zamanı yol verilən mütləq xətanı hesablayın.
Həlli:5,019 ≈ 5,02 (yüzdə birə qədər yuvarlaqlaşdırma). Bu zaman ədəd 0,001 qədər artmışdır, yəni mütləq xəta: |5,019 – 5,02| = 0,001 olmuşdur. 5,019 ≈ 5 (onda birə qədər yuvarlaqlaşma). Bu zaman ədəd 0,019 qədər azalmışdır, yəni mütləq xəta: |5,019 – 5| = 0,019 olmuşdur.