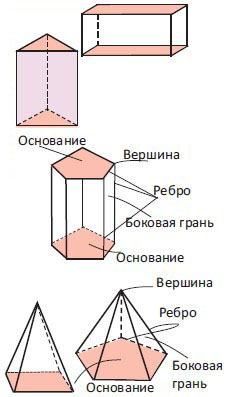
Призма пространственная фигура, у которой есть две параллельные грани (основания), а остальные грани являются боковыми гранями. Призма называется по форме многоуголь ника в основании. Количество боковых граней меняется в зависимости от количества сторон многоуголь ника в основании. Например, у призмы, в основании которой треугольник, боковая поверхность состоит из 3-х граней, а 2 грани - основания, у призмы, в основании которой лежит пятиугольник, - 5 боковых граней. То есть, ёе поверхность состоит из 7 граней (2 оснований и 5 боковых). Если основания и боковые грани призмы являются прямоугольниками, то эту призму называют прямоугольным параллелепипедом.
Пирамида - пространственная фигура с любым многоугольником в основании. Боковые грани пирамиды - треугольники с общей вершиной. Пирамиды получают свое название по форме многоугольника, лежащего в основании: четырехугольная пирамида, треугольная пирамида и т.д.